CIS580 computer vision
Homography
Homogenous Coordinates are a system of coordinates used in the projective space.
The projective space can be imagined as a plane located at Z = 1 in the 3D space. Lines that cut through the origin of the 3D space and intersect the Z = 1 plane form points in the projective space.
A line is a plane of rays through origin. (a,b,c) is a normal vector to the plane.
Point-Line Duality

Horizon
The horizon gives us the orientation of the ground plane with respect to the carmera. This is a line composed by all paralle line in one plane of R3
Recover intrinsics from 3 vanishing points
We consider the simple case where the intrinsic matrix of a camera takes the following form: K =[f 0 u0 0 f v0 0 0 1]
Recover the image center from the projections of three orthogonal vanishing points?

Theorem: The image center (u0, v0) is the orthocenter of the triangle formed by the projections of three orthogonal vanishing points.
Proof: See figure 2. Let C = (u0, v0, 1) denote the homogeneous coordinates of the image center: it is defined as the intersection of image plane V1V2V3 with the optical axis, which is the line through O and perpendicular to V1V2V3.
OC ⊥ V1V2V3 ⇒OCV1 ⊥ V1V2V3 OV1 ⊥ OV2 ⇒OCV1 ⊥ any line contained in V1V2V3
In particular OCV1 ⊥ V2V3. Moreover, OV1 ⊥ OV2, therefore OCV1 ⊥ OV2V3. When two planes are perpendicular, their intersections with a third plane are also perpendicular. Therefore, the intersection of OCV1 with V1V2V3 is perpendicular to intersection of OV2V3 with V1V2V3.
In other words V1C ⊥ V2V3. A similar reasoning leads to V2C ⊥ V3V1 and V3C ⊥ V1V2, therefore C is the orthocenter of V1V2V3.

This elegant result would enable one to calibrate a camera using only the vanishing points in an image. In practice we don’t use this method because it is reliable only when there is a strong perspective in the image, i.e. when vanishing points have low coordinates. When it is not the case, the intersection of parallel lines projected in the image have large coordinates (thousands of pixels), and the relative error is too big to guarantee precise calibration.
Retrieve camera pose
PNP
We can estimate the camera pose from an AprilTag based on homog- raphy estimation iff we have 4 coplaner points.
P3P
P3P方法是众多解决PnP问题中的一种方案,是通过已知的3对精准匹配的2D-3D点求解图像间相对的位姿变换的一种方法,所用到的信息较少。我们首先需要知道的是P3P并不是直接根据2D-3D点求出相机位姿矩阵,而是先求出对应的2D点在当前相机坐标系下的3D坐标,然后根据世界坐标系下的3D坐标和当前相机坐标系下的3D坐标通过ICP信息求解相机位姿的。
这段话来自:https://blog.csdn.net/ABC1225741797/article/details/108066505
The detial calculation is shown in the following link. Ref: https://haralick-org.torahcode.us/journals/three_point_perspective.pdf
#### Procrustes is used to calibrated the Rotation matrix Since the R is not a orthnology and its det may not equal to, so Procrustes should be performed to minimize the error bewteen R with SO3. Y = RX + T Y describes the 3D points in camera frame, X describes the same 3D points in world frame. At lesat 3 correspondences are required R is the rotation of camera frame w.r.t the world frame, and T is the translation form camera frame w.r.t the world frame. These two information tell us where the camera is in the world frame, so called camera pose.

Projective Transformation, Affine transfomration, and Perspective Transformation

Midterm review
PnP vs. SfM
PnP: We know the 2D -> 3D coordniate pairs, calibrated coordinates and world coordinates.
Structure from Motion: only two calibrated coordinates of the same 3D point. 4 unknowns: R, T \lambda and \niu

Epipolar Constraint
Remove the depth from constraint
 https://web.eecs.umich.edu/~justincj/teaching/eecs442/WI2021/assignments/hw6.pdf
https://web.eecs.umich.edu/~justincj/teaching/eecs442/WI2021/assignments/hw6.pdf
Essential Matrix E
The essential matrix encodes epipolar geometry. Given a point in one image, multiplying by the essential matrix will tell us the epipolar line in the second view, Ep = l_{q}
Essential Matrix vs Homography
Homography maps a point ot a point (projective transformation). Essential matrix maps a point to a line (perspective transformation).
Understanding of Epipolar Constraint

Solve E with 8 point correspondences



𝐸 is a singular matrix (Because 𝐸 = #𝑇𝑅, and det #𝑇 = 0)
So smallest singular value is indeed zero!
So, 𝜎1(𝐸) = 𝜎2(𝐸) = ||𝑇|| and 𝜎3 𝐸 = 0
Side note: the ‘third singular vector’ of 𝐸 (null vector because 𝜎!= 0) is nothing but
the translation vector 𝑇 because:
𝐸𝐸"𝑇 = -𝑇-𝑇"𝑇 = 𝑇× −𝑇×𝑇 = 0!
So we already know 𝑻 in terms of 𝑬! (the 3rd left singular vector of 𝑬)

Optical flow
The motion of each pixel in between two frames is called optical flow
Note: we are not showing correspondences for every pixel
Optical Flow Over Patches: Let’s match small local regions (“patches”) between the two images.
(Assumption: All pixels within a patch move in the same way 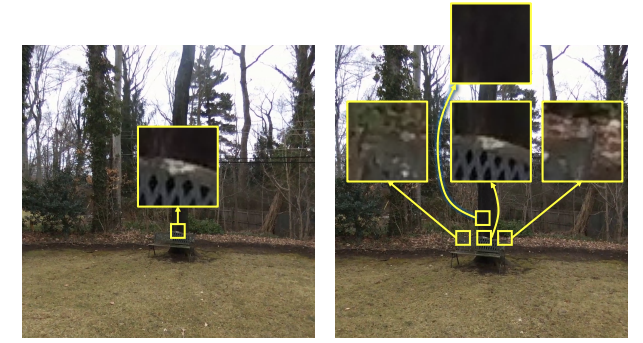 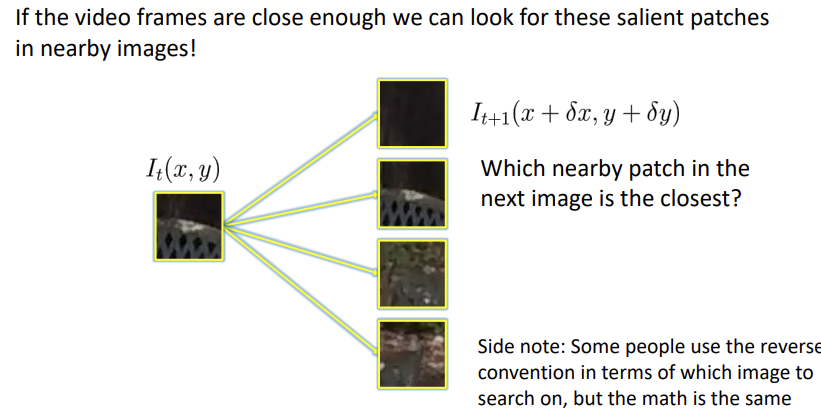 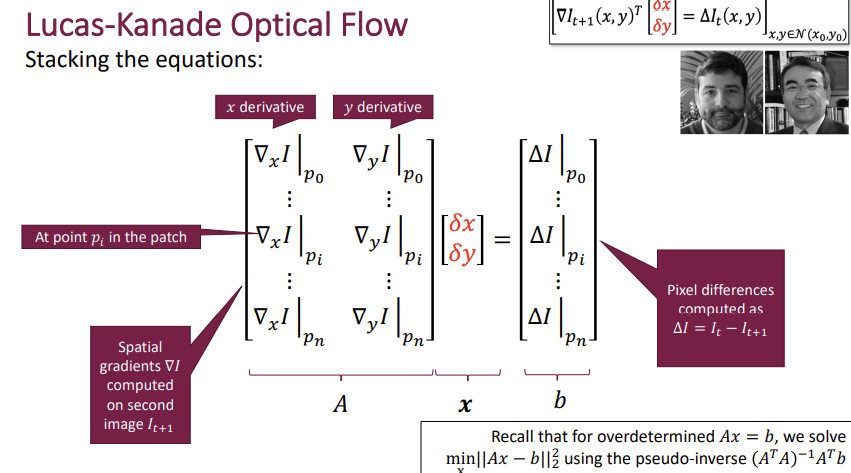 #### Assumptions:  #### Issue: 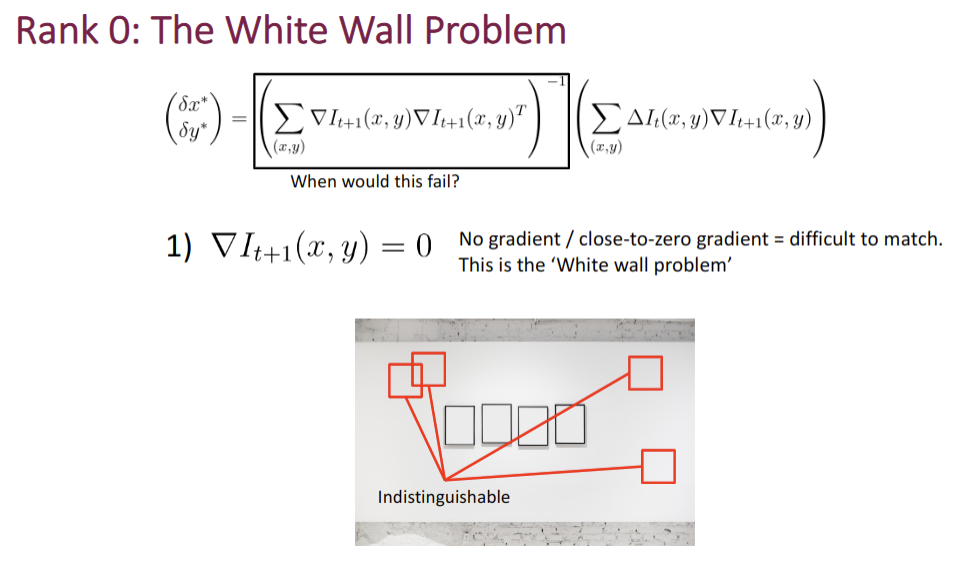     
RANSAC


3D Recon
Unprojection

GRU融合结果

Coarse to fine
